Source: Safalta.com
We frequently see and interact with rectangular-shaped objects in our daily lives, including tables, books, boxes, mobile phones, walls, cricket fields, TV or computer screens, furniture, mattresses, almirahs, and doors. For a better understanding of the principles of the rectangle, we will explore the rectangle, its qualities, the area of a rectangle, formulas, the perimeter of a rectangle, and some solved problems based on it in this article. If you are preparing for competitive exams and looking for expert guidance, you can download our General Knowledge Free Ebook Download Now.Current Affairs Ebook Free PDF: Download Here
Attempt Free Mock Tests- Click Here
Table of content
- Rectangle
- Rectangle: Area
- Rectangle: Shape
- Rectangle: Area Formula
- Rectangle Area: Diagnol used
- Formula of rectangle
- Formula of Rectangle Perimeter
- Properties of rectangle
- Rectangle: Solved Examples
Rectangle
Any closed, two-dimensional figure with four sides whose opposite sides and angles are equal is said to be a rectangle.
The opposing parties perceive a parallel in the fact that they never interact.
All four internal angles of a rectangle are 90 degrees.
In the illustration below, you can see the rectangle's sides and angles.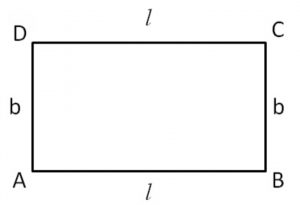
In the above figure, a rectangle ABCD is shown having sides in which the length of sides AB = CD = l, AD = BC = b, and AD || BC, AB || CD. The values of internal angles are 90°.
Rectangle: Area
The space contained within a rectangle's four edges is known as its area. The area of a rectangle can be calculated mathematically by counting the number of unit squares that can fit inside it. We see many rectangular things in our daily lives, thus determining their areas is also necessary. Numerous rectangular things, including books, tables, laptop screens, CPUs, etc., serve as examples. Only the length and width of a rectangle's rectangle determine its area. The formula shine below can be used to get the rectangle's area. In terms of square units, a rectangle's area is expressed as sq. m, sq. cm, or sq. mm.Area of rectangle = length × breadth
A = l × B Square units
Rectangle: Shape
As we've already discussed, a rectangle is a closed, two-dimensional figure with four sides. The rectangle contains four internal angles that are each equal to 90 degrees and opposite sides that are equal and parallel to one another. We frequently come with rectangular objects, such as walls, crates, tables, mattresses, laptops computer screens, and more.Rectangle: Area Formula
The space contained inside the rectangle's outer perimeter is referred to as its area. The product of length and width can be used to compute the rectangle's area. The formula to determine a rectangle's area is the product of its length and width. For example, if a rectangle's length is l, its breadth is b, and its area is denoted by A. A rectangle's area is expressed in square units.Area of rectangle = length × breadth
A = l × b square units
Rectangle Area: Diagnol used
As will be covered later, diagonals can also be used to calculate the area of a rectangle.- (Diagonal)2 = (Length)2 + (Width)2
- (Length)2 = (Diagonal)2 – (Width)2
- Length = √ (Diagonal)^2 – (Width)^2
- (Width)2 = (Diagonal)2 – (Length)2
- Width = √(Diagonal)^2 – (length)^2
- We know that the area of a rectangle is the product of length and breadth
- Area of rectangle = length × breadth
- Area of rectangle = length × √(Diagonal)^2 – (Length)^2
- or Area of rectangle = √ (Diagonal)^2 – (Width)^2 × width
Formula of rectangle
The above discussion goes into great detail on how to compute a rectangle's area. The formula for calculating a rectangle's area is to multiply the rectangle's length and width by their respective magnitudes. Let L be the length, W be the width, and A be the area of the rectangle. The rectangular area formula is thus expressed as:A = L × W square units
Formula of Rectangle Perimeter
The sum of a rectangle's outer bounds is known as its perimeter. It is equal to the rectangle's length plus width multiplied by two. The value of a rectangle's parameter is obtained by adding the perimeter, which is a linear measurement of the rectangle's exterior sides. It is described using length units like m, cm, or mm.Take into consideration the rectangle ABCD, which has the dimensions l and b. The perimeter of the rectangle ABCD is denoted by
The perimeter of the rectangle = 2 (l + b)
Properties of rectangle
Numerous characteristics of a rectangle are employed in geometry and other contexts where it is stated. Below is a list of the rectangle's key attributes.- An example of a quadrilateral is a rectangle.
- A rectangle's opposite sides are equal and parallel to one another.
- Each vertex of a rectangle has an internal angle of 90°.
- Rectangles' internal angles add up to 360° (90°+90°+90°+90°).
- A rectangle's diagonals cut each other in half.
- A rectangle's two diagonals are of equal length.
- The Pythagoras theorem can be used to determine the length of the diagonals. When the diagonal's sides are a and b, its length is equal to (a2 + b2).
- A rectangle is also referred to as a parallelogram since its sides are parallel.
- All parallelograms are absolutely rectangles, but not all rectangles are parallelograms.
Rectangle: Solved Examples
1. If the length of a rectangle is 8cm and the breadth measures 5cm. Find the area of a rectangle.
Solution: Given l = 8cm and b = 5cm
then the area of rectangle A = l × b
A = 8 × 5
A = 40 sq. cm
2. The length and breadth of a rectangular courtyard are 75 m and 32 m.
Find the cost of leveling it at the rate of $3 per m2.
Also, find the distance covered by a boy to take 4 rounds of the courtyard.
Solution: Length of the courtyard = 75 m
The breadth of the courtyard = is 32 m
The perimeter of the courtyard = 2 (75 + 32) m
= 2 × 107 m
= 214 m
Distance covered by the boy in taking 4 rounds = perimeters of the courtyard
= 4 × 214
= 856 m
We know that the area of the courtyard = length × breadth
= 75 × 32 m22
= 2400 m22
For 1 m22, the cost of leveling = $3
For 2400 m22, the cost of leveling = $3 × 2400
= $7200
3. Shyam has a rectangular photo frame that is 9 inches long and 5 inches wide. Help Shyam in finding the area of the photo frame.
Solution: We know the formula to calculate the area of a rectangle
Area of a Rectangle = (Length × Width).
Thus, the area of the rectangular frame = 9 × 5 = 45 square inches
Therefore, the area of the photo frame = 45 square inches
4. Find the perimeter and area of the rectangle o with a length of 17 cm and a breadth of 13 cm.
Solution: Given length = 17 cm, breadth = 13 cm
The perimeter of the rectangle = 2 (length + breadth)
= 2 (17 + 13) cm
= 2 × 30 cm
= 60 cm
We know that the area of the rectangle = length × breadth
= (17 × 13) cm2
= 221 cm2
5. A wire in the shape of a rectangle of length 35 cm and breadth of 18 cm is rebent to form a square. What will be the measure of each side?
Solution: The perimeter of the rectangle = 2 (35 + 18) cm
= 2 × 53
= 106 cm
The Perimeter of the square of side x cm = the, Therefore, the perimeter of the rectangle = Perimeter of the Square
106 cm = 4x
⇒ x = 26.5
Therefore, each side of the square = 26.5 cm
What are the 7 properties of rectangle?
The fundamental properties of rectangles are:- A rectangle is a quadrilateral.
- The opposite sides are parallel and equal to each other.
- Each interior angle is equal to 90 degrees.
- The sum of all the interior angles is equal to 360 degrees.
- The diagonals bisect each other.
- Both the diagonals have the same length.
