The seventh chapter in Mathematics textbook is 'Coordinate Geometry'.
- Position of a point P in the Cartesian plane with respect to co-ordinate axes is represented by the ordered pair (x, y).
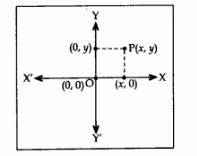
- The line X’OX is called the X-axis and YOY’ is called the Y-axis.
- The part of intersection of the X-axis and Y-axis is called the origin O and the co-ordinates of O are (0, 0).
- The perpendicular distance of a point P from the Y-axis is the ‘x’ co-ordinate and is called the abscissa.
- The perpendicular distance of a point P from the X-axis is the ‘y’ co-ordinate and is called the ordinate.
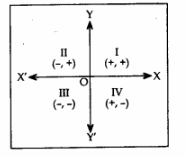
- Signs of abscissa and ordinate in different quadrants are as given in the diagram:
- Any point on the X-axis is of the form (x, 0).
- Any point on the Y-axis is of the form (0, y).
The topics discussed in this chapter are as follows:
- Points on a Cartesian Plane
- Distance Formula
- Section Formula
- Mid point
- Points of Trisection
- Centroid of a Triangle
- Area from Coordinates
Students can view and download the chapter from the link given below.
Click here to get the complete chapter
NCERT Solutions for Chapter 7: Coordinate Geometry
Also Check
Chapter 1: Real Numbers
Chapter 2: Polynomials
Chapter 3: Pair of Linear Equations in Two Variables
Chapter 4: Quadratic Equations
Chapter 5: Arithmetic Progression
Chapter 6: Triangles
Chapter 8: Introduction to Trigonometry
Chapter 9: Some Applications of Trigonometry
Chapter 10: Circle
Chapter 11: Constructions
Chapter 12: Areas Related to Circles
Chapter 13: Surface Areas and Volume
Chapter 14: Statistics
Chapter 15: Probability
Check out Frequently Asked Questions (FAQs) for Chapter 7: Coordinate Geometry
The midpoint of a line segment joining two points A(2, 4) and B(-2, -4) is
As per midpoint formula, we know;
x-coordinate of the midpoint = [2 + (-2)]/2 = 0/2 = 0
y-coordinate of the midpoint = [4 + (-4)]/2=0/2=0
Hence, (0, 0) is the midpoint of AB.
The distance of point A(2, 4) from the x-axis is
The distance of a point from the x-axis is equal to the ordinate of the point which is 4 units.
The point which divides the line segment of points P(-1, 7) and (4, -3) in the ratio of 2:3 is
By section formula we know:
x = [(2 × 4) + (3 × (-1))]/(2 + 3) = (8 – 3)/5 = 1
y = [(2 × (-3)) + (3 × 7)]/(2 + 3) = (-6 + 21)/5 = 3
Hence, the required point is (1, 3).
The coordinates of a point P, where PQ is the diameter of a circle whose centre is (2, – 3) and Q is (1, 4) is
By midpoint formula, we know;
[(x + 1)/2, (y + 4)/2] = (2, -3) {since, O is the midpoint of PQ}By equating the corresponding coordinates,
(x + 1)/2 = 2
x + 1 = 4
x = 3
And
(y + 4)/2 = -3
y + 4 = -6
y = -10
So, the coordinates of point P is (3, -10).
The distance of the point P(–6, 8) from the origin is
We know that the distance of a point P(x, y) from the origin is √(x2 + y2).
Thus, the distance of the point P(-6, 8) from the origin = √[(-6)2 + (8)2]
= √(36 + 64)
= √100
= 10 units
