Mensuration is a very important topic under Quantitative Aptitude for competitive exams. There are different formulas to solve questions from this section.
You can also check ,
| Speed, Time and Distance | Missing Term |
| Parajumble | Odd One Out |
| Blood Relations | Syllogism |
| Ratio and Proportion | Time And Work |
Mensuration Formula – Simple Figures
Formulas given here are only for 2 dimensional simple figures, one must learn the properties and other aspects in detail. For 3-dimensional figures stay tuned with Safalta.
| Shapes | Area(A) | Perimeter(P) | Diagonal(d) | Nomenclature |
|---|---|---|---|---|
| Square | a2 | 4a | √2a | Side = a |
| Rectangle | l x b | 2(l+b) | √2 (l2+b2) | Length = l Breadth = b |
| Rhombus | ½ × d1 × d2 | 4a | 2A/d2 | Diagonals = d1 and d2 |
| Parallelogram | p x h | 2(p+q) | √(p2+q2-2pqcosβ) | Base = p Side = q Angle = β |
| Circle | πr2 (πr2)/2 (for semi-circle) | 2πr R(π+2 (for semi-circle) |
Also Read:
Important Mensuration Questions and Answers For Competitive Exams
Q1. A rectangle has 20 cm as its length and 320 sq cm as its area. Its area is increased to 1 ¼ times its original area by increasing only its length. Its new perimeter ( in cm ) is
80
82
85
90
None of the above
Q2. The diagonal of a rectangular field is 50 m and one of the sides is 40 m. If the cost of cutting the grass of the field is Rs. 27 per square metre then the total cost of cutting all grass of the rectangular field is
Rs 32800
Rs 35000
Rs 32400
Rs 32000
None of the above
Q3. Four cows are tied to each corner of a square field of side 7 cm. The cows are tied with a rope such that each cow grazes maximum possible field and all the cows graze equal areas. Find the area of the un-grazed field.
10.5 cm2
11.5 cm2
38.5 cm2
49 cm2
None of the above
Q4. The area of a rectangle is four times of a square. The length of the rectangle is 80 cm and the breadth of the rectangle is 3 times that of the side of the square. What is the side ( in cm ) of the square?
50 cm
55cm
60 cm
40 cm
65 cm
Q5. The ratio between the perimeter and the breadth of a rectangle is 5 : 1. If the area of the rectangle is 216 sq. cm, what is the length of the rectangle?
10cm
15 cm
18 cm
21 cm
24 cm
Q6. A contractor undertakes a job of fencing a rectangular field of length 100 m and breadth 50 m. The cost of fencing is Rs. 2 per metre and the labour charges are Re. 1 per metre, both paid directly to the contractor. Find the total cost of fencing if 10 % of the amount paid to the contractor is paid as tax to the land authority.
Rs 900
Rs 910
Rs 990
Rs 1000
Rs 1100
Q7. A square of perimeter 88cm and a circle of perimeter 88cm are given. Which figure has larger area and by how much?
125 cm2
128 cm2
132 cm2
135 cm2
136 cm2
Q8. The areas of a square and a rectangle are equal. The length of the rectangle is greater than the length of any side of the square by 4cm and the breadth is less by 3cm. Find the perimeter of the rectangle.
40 cm 45 cm 50 cm 60 cm 80 cm Q9. A wire is bent in the shape of square of area 324cm2. If the same wire is bent in the form of a semicircle, the radius of the semicircle is- 1) 10 cm 12 cm
14 cm
16 cm
None of the above
Q10. A kite is in the shape of a square with a diagonal 48cm attached to a triangle of the base 4cm and height 6cm. How much paper has been used to make it? 1) 200 cm2
250 cm2
300 cm2
325 cm2
400 cm2



be 3.5 cm.
=> Area grazed by 1 cow = (π x Radius2 x θ) / 360
=> Area grazed by 1 cow = (π x 3.52 x 90) / 360 = (π x 3.52) / 4 => Area grazed by 4 cows = 4 x [(π x 3.52) / 4] = π x 3.52
=> Area grazed by 4 cows = 38.5 cm2
Now, area of square field = Side2 = 72 = 49 cm2

Q5.
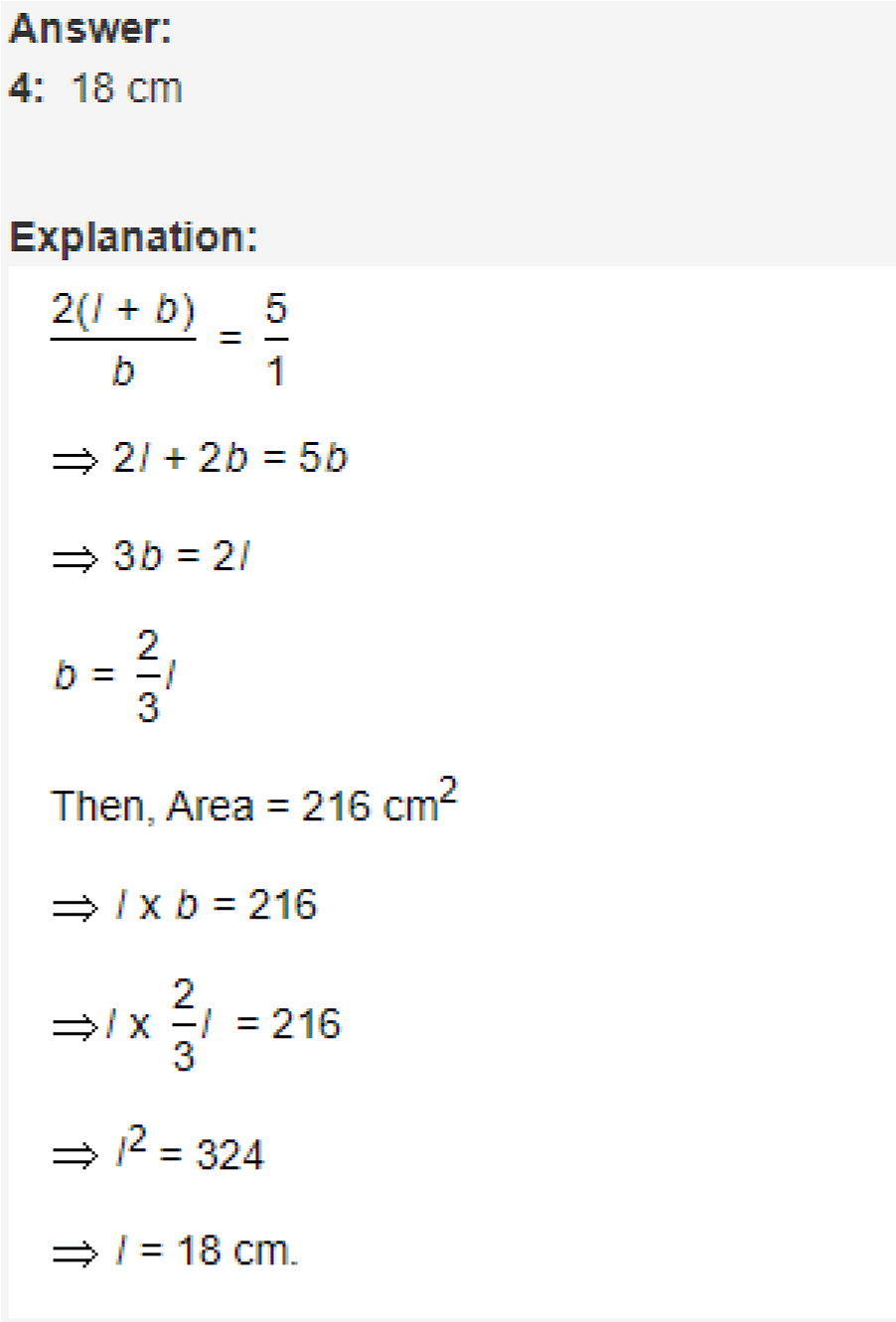
Q6. Solution : Total cost of fencing per metre = Rs. 2 + 1 = Rs. 3
Length of fencing required = Perimeter of the rectangular field = 2 (Length + Breadth)
=> Length of fencing required = 2 x (100 + 50) = 300 metre
=> Amount paid to the contractor = Rs. 3 x 300 = 900
=> Amount paid to the land authority = 10 % of Rs. 900 = Rs. 90 therefore, total cost of fencing = Rs. 900 + 90 = Rs. 990
Q7. Solution: Perimeter of square =88 cm
4 x side = 88, side = 22
Area of square = (22)2 = 484 cm2
Circumference of circle =88cm 2π(radius) = 88 radius = 44*7/22 = 14 Area of circle = π (radius)2
=22/7 * 14 * 14 = 616 cm2
Area of circle – Area of square = 616 – 484 = 132 cm2 Hence, circle has larger area than square by 132 cm2
Q8. Solution: Let the side of square is a, then length of rectangle is a+4 breadth of
rectangle is a-3
Acc. to question –
Area of square = Area of rectangle a2 = (a+4)(a-3) a2 + 4a – 3a – 12 = 0
a = 12
Perimeter of rectangle = 2(l+b)
=2(16 + 9) =50 cm
Hence, perimeter of rectangle is 50 cm
Q9. Solution: Let the side of the square is a. a2 = 324, a = 18 Perimeter of the square = 4 x 18 = 72 cm Let radius of the semicircle is r.
Perimeter of the semicircle = 2r + πr
Acc to question 2r + πr = 72 r(2 + 22/7)= 72
r = 72 * 7 /36 r
=14 cm
Hence radius of the semicircle is 14cm
Q10. Solution: Area of square = 1/2(diagonal)2
=1/2 * (24)2
=288 cm2
Area of triangle = 1/2 * base * height
= 1/2 * 4 * 6 = 12 cm2
Total area = 288 + 12 = 300 cm2
Mensuration and geometry has important place in competitive exams. It not only constitutes an important section on its own, but also knowledge of Mensuration is important for tackling data interpretation section. Hence student is advised to go through the important mensuration questions and answers completely and thoroughly. Student is advised to remember the formulas involved and regular revision will be of help. We hope the above questions were helpful in giving you a understanding of this topic and the questions involved.



